MATHEMATICAL MODELING AND ANALYSIS OF HUMAN TO HUMAN SHIGELLOSIS TRANSMISSION WITH PUBLIC ENLIGHTENMENT

Abstract

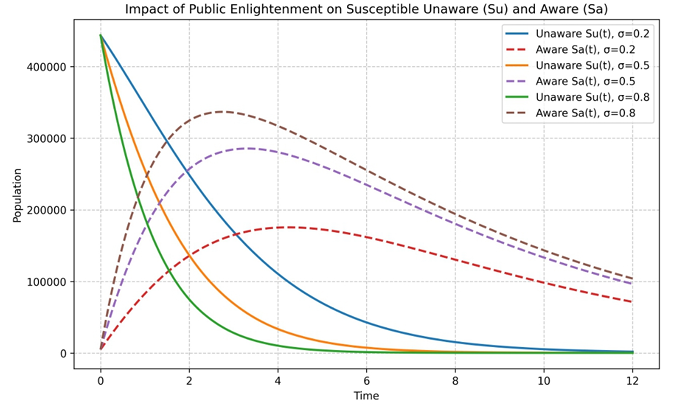
The shigella bacterium spreads a disease of the digestive tract known as shigellosis. The primary means of preventing shigellosis have historically been better sanitation and hygiene measures. Every year, this disease claims the lives of almost 1.1 million people, children under five years of age being the most affected. In this paper a deterministic mathematical model is proposed describing the transmission dynamics of human to human shigellosis. The model exhibits two equilibrium states, the disease-free equilibrium and the endemic equilibrium. However, the disease free equilibrium state is shown to be both locally and globally asymptotically stable under certain conditions when the control reproduction is less than unity (R_c<1). In contrast, endemic equilibrium is found to be globally asymptotically stable when the control reproduction number is greater than unity (R_c>1). The most sensitive parameters for the control of the spread of shigellosis are identified by the forward sensitivity index method (one that is very effective for the control of the disease). The contact rate B is found to be the most sensitive among all the parameters, indicating that to avoid the persistence of the disease, reducing contact between individuals should be emphasized. Finally, we obtained some numerical simulation results which that show that to eradicate shigellosis, there is need for minimizing  the contact between infected individuals and susceptible ones and also minimize the number of carriers individuals that progressing to infected compartment when combined with public enlightenment and isolation of infected individuals.